Written on 19.48 by sianturikomkom
The quantity
work has to do with a force causing a displacement. Work has nothing to do with the amount of time that this force acts to cause the displacement. Sometimes, the work is done very quickly and other times the work is done rather slowly. For example, a rock climber takes an abnormally long time to elevate her body up a few meters along the side of a cliff. On the other hand, a trail hiker (who selects the easier path up the mountain) might elevate her body a few meters in a short amount of time. The two people might do the same amount of work, yet the hiker does the work in considerably less time than the rock climber. The quantity that has to do with the rate at which a certain amount of work is done is known as the power. The hiker has a greater
power rating than the rock climber.
Power is the rate at which work is done. It is the work/time ratio. Mathematically, it is computed using the following equation.
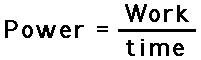

The standard metric unit of power is the
Watt. As is implied by the equation for power, a unit of power is equivalent to a unit of work divided by a unit of time. Thus, a Watt is equivalent to a Joule/second. For historical reasons, the
horsepower is occasionally used to describe the power delivered by a machine. One horsepower is equivalent to approximately 750 Watts.
Most machines are designed and built to do work on objects. All machines are typically described by a power rating. The power rating indicates the rate at which that machine can do work upon other objects. Thus, the power of a machine is the work/time ratio for that particular

machine. A car engine is an example of a machine that is given a power rating. The power rating relates to how rapidly the car can accelerate the car. Suppose that a 40-horsepower engine could accelerate the car from 0 mi/hr to 60 mi/hr in 16 seconds. If this were the case, then a car with four times the horsepower could do the same amount of work in one-fourth the time. That is, a 160-horsepower engine could accelerate the same car from 0 mi/hr to 60 mi/hr in 4 seconds. The point is that for the same amount of work, power and time are inversely proportional. The power equation suggests that a more powerful engine can do the same amount of work in less time.
A person is also a machine that has a
power rating. Some people are more power-full than others. That is, some people are capable of doing the same amount of work in less time or more work in the same amount of time. A common physics lab involves quickly climbing a flight of stairs and using mass, height and time information to determine a student's personal power. Despite the diagonal motion along the staircase, it is often assumed that the horizontal motion is constant and all the force from the steps is used to elevate the student upward at a constant speed. Thus, the weight of the student is equal to the force that does the work on the student and the height of the staircase is the upward displacement.

Suppose that Ben Pumpiniron elevates his 80-kg body up the 2.0-meter stairwell in 1.8 seconds. If this were the case, then we could calculate Ben's
power rating. It can be assumed that Ben must apply an 800-Newton downward force upon the stairs to elevate his body. By so doing, the stairs would push upward on Ben's body with just enough force to lift his body up the stairs. It can also be assumed that the angle between the force of the stairs on Ben and Ben's displacement is 0 degrees. With these two approximations, Ben's power rating could be determined as shown below.
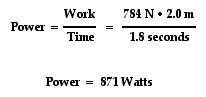
Ben's power rating is 871 Watts. He is quite a
horse.
The expression for power is work/time. And since the expression for work is force*displacement, the expression for power can be rewritten as (force*displacement)/time. Since the expression for velocity is displacement/time, the expression for power can be rewritten once more as force*velocity. This is shown below.


This new equation for power reveals that a powerful machine is both strong (big force) and fast (big velocity). A powerful car engine is strong and fast. A powerful piece of farm equipment is strong and fast. A powerful weightlifter is strong and fast. A powerful lineman on a football team is strong and fast. A
machine that is strong enough to apply a big force to cause a displacement in a s

|
Written on 18.29 by sianturikomkom
Work done by a constant force
When the point at which a force acts moves, the force is said to have done work.
When the force is constant, the work done is defined as the product of the force and distance moved.

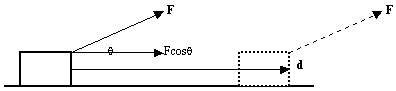
Consider the example in Figure 3.1, a force F acting at the angle
q moves a body from point A to point B.

Figure 3.1: Notation for work done by a force The distance moved in the direction of the force is given by

So the work done by the force F is

If the body moves in the same direction as the force the angle is 0.0 so
Work done = Fs When the angle is 90 then the work done is zero.
The SI units for work are Joules
J (with force,
F, in Newton's
N and distance,
s, in metres
m).
Worked Example 3.1
How much work is done when a force of 5 kN moves its point of application 600mm in the direction of the force.
Solution

Worked Example 3.2
Find the work done in raising 100 kg of water through a vertical distance of 3m.
Solution
The force is the weight of the water, so

Work done by a variable force
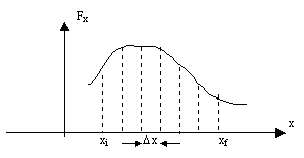
Forces in practice will often vary. In these cases Equation 3.1 cannot be used. Consider the case where the force varies as in Figure 3.2
For the thin strip with width ds - shown shaded in Figure 3.2 - the force can be considered constant at
F. The work done over the distance ds is then

This is the area of the shaded strip.
The total work done for distance
s is the sum of the areas of all such strips. This is the same as the area under the Force-distance curve.

Figure 3.2: Work done by a variable force So for a variable force

Equation 3.2
Clearly this also works for a constant force - the curve is then a horizontal line. In general you must uses some special integration technique to obtain the area under a curve. Three common techniques are the trapezoidal, mid-ordinate and Simpson's rule. They are not detailed here but may be found in many mathematical text book.
Energy
A body which has the capacity to do work is said to possess energy.
For example , water in a reservoir is said to possesses energy as it could be used to drive a turbine lower down the valley. There are many forms of energy e.g. electrical, chemical heat, nuclear, mechanical etc.
The SI units are the same as those for work, Joules
J.
In this module only purely mechanical energy will be considered. This may be of two kinds,
potential and
kinetic.
Potential Energy
There are different forms of potential energy two examples are: i) a pile driver raised ready to fall on to its target possesses gravitational potential energy while (ii) a coiled spring which is compressed possesses an internal potential energy.
Only gravitational potential energy will be considered here. It may be described as energy due to position relative to a standard position (normally chosen to be he earth's surface.)
The potential energy of a body may be defined as the amount of work it would do if it were to move from the its current position to the standard position.
Formulae for gravitational potential energy
A body is at rest on the earth's surface. It is then raised a vertical distance
h above the surface. The work required to do this is the force required times the distance
h.
Since the force required is it's weight, and weight,
W = mg, then the work required is
mgh.
The body now possesses this amount of energy - stored as potential energy - it has the capacity to do this amount of work, and would do so if allowed to fall to earth.
Potential energy is thus given by:

Equation 3.3
where
h is the height above the earth's surface.
Worked example 3.3
What is the potential energy of a 10kg mass:
- 100m above the surface of the earth
- at the bottom of a vertical mine shaft 1000m deep.
Solution a)

b)
 Kinetic energy
Kinetic energy
Kinetic energy may be described as energy due to motion.
The kinetic energy of a body may be defined as the amount of work it can do before being brought to rest.
For example when a hammer is used to knock in a nail, work is done on the nail by the hammer and hence the hammer must have possessed energy.
Only linear motion will be considered here.
Formulae for kinetic energy
Let a body of mass
m moving with speed
v be brought to rest with uniform deceleration by a constant force
F over a distance
s.
Using Equation 1.4

And work done is given by

The force is
F = ma so

Thus the kinetic energy is given by

Kinetic energy and work done
When a body with mass
m has its speed increased from
u to
v in a distance
s by a constant force
F which produces an acceleration
a, then from Equation 1.3 we know

multiplying this by
m give an expression of the increase in kinetic energy (the difference in kinetic energy at the end and the start)

Thus since
F = ma

but also we know

So the relationship between kinetic energy can be summed up as
Work done by forces acting on a body = change of kinetic energy in the body Equation 3.5
This is sometimes known as the work-energy theorem.
Worked example 3.4
A car of mass 1000 kg travelling at 30m/s has its speed reduced to 10m/s by a constant breaking force over a distance of 75m.
Find:
- The cars initial kinetic energy
- The final kinetic energy
- The breaking force
Solution a)

b)

c)
Change in kinetic energy = 400 kJ By Equation 3.5 work done = change in kinetic energy so

Conservation of energy
The principle of conservation of energy state that the total energy of a system remains constant. Energy cannot be created or destroyed but may be converted from one form to another.
Take the case of a crate on a slope. Initially it is at rest, all its energy is potential energy. As it accelerates, some of it potential energy is converted into kinetic energy and some used to overcome friction. This energy used to overcome friction is not lost but converted into heat. At the bottom of the slope the energy will be purely kinetic (assuming the datum for potential energy is the bottom of the slope.)
If we consider a body falling freely in air, neglecting air resistance, then
mechanical energy is conserved, as potential energy is lost and equal amount of kinetic energy is gained as speed increases.
If the motion involves friction or collisions then the principle of conservation of energy is true, but conservation of mechanical energy is not applicable as some energy is converted to heat and perhaps sound.
Worked Example 3.5
A cyclist and his bicycle has a mass of 80 kg. After 100m he reaches the top of a hill, with slope 1 in 20 measured along the slope, at a speed of 2 m/s. He then free wheels the 100m to the bottom of the hill where his speed has increased to 9m/s.
How much energy has he lost on the hill?
Solution

Figure 3.3: Dimensions of the hill in worked example 3.5 If the hill is 100m long then the height is:

So potential energy lost is

Increase in kinetic energy is

By the principle of conservation of energy


Power
Power is the rate at which work is done, or the rate at which energy is used transferred.

Equation 3.6
The SI unit for power is the watt
W. A power of 1
W means that work is being done at the rate of 1
J/s.
Larger units for power are the kilowatt
kW (1
kW = 1000
W = 10
3 W) and
the megawatt
MW (1
MW = 1000000
W = 10
6 W).
If work is being done by a machine moving at speed
v against a constant force, or resistance,
F, then since work doe is force times distance, work done per second is
Fv, which is the same as power.

Equation 3.7
Worked Example 3.6
A constant force of 2kN pulls a crate along a level floor a distance of 10 m in 50s.
What is the power used?
Solution


Alternatively we could have calculated the speed first

and then calculated power
 Worked Example 3.7
Worked Example 3.7
A hoist operated by an electric motor has a mass of 500 kg. It raises a load of 300 kg vertically at a steady speed of 0.2 m/s. Frictional resistance can be taken to be constant at 1200 N.
What is the power required?
Solution


From Equation 3.7

Worked example 3.8
A car of mass 900 kg has an engine with power output of 42 kW. It can achieve a maximum speed of 120 km/h along the level.
- What is the resistance to motion?
- If the maximum power and the resistance remained the same what would be the maximum speed the car could achieve up an incline of 1 in 40 along the slope?
Solution 
Figure 3.4: Forces on the car on a slope in Worked Example 3.8 First get the information into the correct units:

a) Calculate the resistance

b)


Or in km/h

Moment, couple and torque
The moment of a force
F about a point is its turning effect about the point.
It is quantified as the product of the force and the perpendicular distance from the point to the line of action of the force.

Figure 3.4: Moment of a force In Figure 3.5 the moment of
F about point
O is

Equation 3.8
A
couple is a pair of equal and parallel but opposite forces as shown in Figure 3.6:

Figure 3.6: A couple The moment of a couple about any point in its plane is the product of one force and the perpendicular distance between them:

Equation 3.9
Example of a couple include turning on/off a tap, or winding a clock. The SI units for a moment or a couple are Newton metres,
Nm.
In engineering the moment of a force or couple is know as
torque. A spanner tightening a nut is said to exert a torque on the nut, similarly a belt turning a pulley exerts a torque on the pulley.
Work done by a constant torque
Let a force
F turn a light rod OA with length
r through an angle of
q to position OB, as shown in Figure 3.7.

Figure 3.7: Work done by a constant torque The torque
TQ exerted about O is force times perpendicular distance from O.

Equation 3.10
Now work done by
F is
 s
s is the arc of the circle, when
qis measure in radians


Equation 3.11
The work done by a constant torque
TQ is thus the product of the torque and the angle through which it turns (where the angle is measured in radians.)
As the SI units for work is Joules,
TQ must be in
Nm
Power transmitted by a constant torque
Power is rate of doing work. It the rod in Figure 3.7 rotates at
n revolutions per second, then in one second the angle turned through is

radians, and the work done per second will be, by Equation 3.11

as angular speed is

then

Equation 3.12
The units of power are Watts,
W, with
n in
rev/s,
w in
rad/s and
TQ in
Nm.
Worked Example 3.9
A spanner that is used to tighten a nut is 300mm long. The force exerted on the end of a spanner is 100 N.
- What is the torque exerted on the nut?
- What is the work done when the nut turns through 30° ?
Solution a)
Calculate the torque by Equation 3.10

b)
Calculate the work done by Equation 3.11
 Worked Example 3.10
Worked Example 3.10
An electric motor is rated at 400 W. If its efficiency is 80%, find the maximum torque which it can exert when running at 2850 rev/min.
Solution
Calculate the speed in rev/s using Equation 3.12

Calculate the power as the motor is 80% efficient


Work done by a variable torque
In practice the torque is often variable. In this case the work done cannot be calculated by Equation 3.11, but must be found in a similar way to that used for a variable force (see earlier.)

Figure 3.8: Work done by a variable torque The work done when angular displacement is
dqis
TQdq. This is the area of the shaded strip in Figure 3.8. the total work done for the angular displacement
q is thus the area under the torque/displacement graph.
For variable torque

Equation 3.13
As with variable forces, in general you must uses some special integration technique to obtain the area under a curve. Three common techniques are the trapezoidal, mid-ordinate and Simpson's rule. They are not detailed here but may be found in many mathematical text book.
Worked Example 3.11
A machine requires a variable torque as shown in Figure 3.9, Find:
- The work done per revolution
- The average torque over one revolution
- The power required if the machine operates at 30 rev/min
 Figure 3.9: Torque requirement for Worked Example 3.12 Solution
Figure 3.9: Torque requirement for Worked Example 3.12 Solution
a)
From Equation 3.13

for one revolution
b)
Average torque is the average height of figure OABCDE = area /2
p

c)


|
![]()

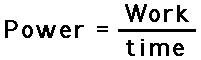

 machine. A car engine is an example of a machine that is given a power rating. The power rating relates to how rapidly the car can accelerate the car. Suppose that a 40-horsepower engine could accelerate the car from 0 mi/hr to 60 mi/hr in 16 seconds. If this were the case, then a car with four times the horsepower could do the same amount of work in one-fourth the time. That is, a 160-horsepower engine could accelerate the same car from 0 mi/hr to 60 mi/hr in 4 seconds. The point is that for the same amount of work, power and time are inversely proportional. The power equation suggests that a more powerful engine can do the same amount of work in less time.
machine. A car engine is an example of a machine that is given a power rating. The power rating relates to how rapidly the car can accelerate the car. Suppose that a 40-horsepower engine could accelerate the car from 0 mi/hr to 60 mi/hr in 16 seconds. If this were the case, then a car with four times the horsepower could do the same amount of work in one-fourth the time. That is, a 160-horsepower engine could accelerate the same car from 0 mi/hr to 60 mi/hr in 4 seconds. The point is that for the same amount of work, power and time are inversely proportional. The power equation suggests that a more powerful engine can do the same amount of work in less time. Suppose that Ben Pumpiniron elevates his 80-kg body up the 2.0-meter stairwell in 1.8 seconds. If this were the case, then we could calculate Ben's power rating. It can be assumed that Ben must apply an 800-Newton downward force upon the stairs to elevate his body. By so doing, the stairs would push upward on Ben's body with just enough force to lift his body up the stairs. It can also be assumed that the angle between the force of the stairs on Ben and Ben's displacement is 0 degrees. With these two approximations, Ben's power rating could be determined as shown below.
Suppose that Ben Pumpiniron elevates his 80-kg body up the 2.0-meter stairwell in 1.8 seconds. If this were the case, then we could calculate Ben's power rating. It can be assumed that Ben must apply an 800-Newton downward force upon the stairs to elevate his body. By so doing, the stairs would push upward on Ben's body with just enough force to lift his body up the stairs. It can also be assumed that the angle between the force of the stairs on Ben and Ben's displacement is 0 degrees. With these two approximations, Ben's power rating could be determined as shown below.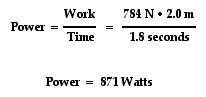




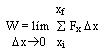
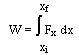
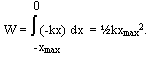
 .
. 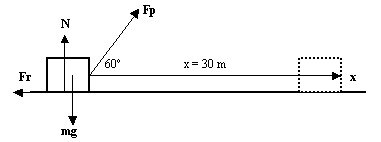



































 Figure 3.9: Torque requirement for Worked Example 3.12
Figure 3.9: Torque requirement for Worked Example 3.12


