Written on 19.13 by sianturikomkom
http://theory.uwinnipeg.ca/physics/work/index.html
http://www.efm.leeds.ac.uk/CIVE/CIVE1140/section03/mechanics_sec03_full_notes02.html
http://hyperphysics.phy-astr.gsu.edu/hbase/work.html
http://www.edinformatics.com/math_science/work_energy_power.html
http://www.sciencejoywagon.com/physicszone/05work-energy/

|
Written on 19.48 by sianturikomkom
The quantity
work has to do with a force causing a displacement. Work has nothing to do with the amount of time that this force acts to cause the displacement. Sometimes, the work is done very quickly and other times the work is done rather slowly. For example, a rock climber takes an abnormally long time to elevate her body up a few meters along the side of a cliff. On the other hand, a trail hiker (who selects the easier path up the mountain) might elevate her body a few meters in a short amount of time. The two people might do the same amount of work, yet the hiker does the work in considerably less time than the rock climber. The quantity that has to do with the rate at which a certain amount of work is done is known as the power. The hiker has a greater
power rating than the rock climber.
Power is the rate at which work is done. It is the work/time ratio. Mathematically, it is computed using the following equation.
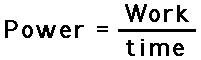

The standard metric unit of power is the
Watt. As is implied by the equation for power, a unit of power is equivalent to a unit of work divided by a unit of time. Thus, a Watt is equivalent to a Joule/second. For historical reasons, the
horsepower is occasionally used to describe the power delivered by a machine. One horsepower is equivalent to approximately 750 Watts.
Most machines are designed and built to do work on objects. All machines are typically described by a power rating. The power rating indicates the rate at which that machine can do work upon other objects. Thus, the power of a machine is the work/time ratio for that particular

machine. A car engine is an example of a machine that is given a power rating. The power rating relates to how rapidly the car can accelerate the car. Suppose that a 40-horsepower engine could accelerate the car from 0 mi/hr to 60 mi/hr in 16 seconds. If this were the case, then a car with four times the horsepower could do the same amount of work in one-fourth the time. That is, a 160-horsepower engine could accelerate the same car from 0 mi/hr to 60 mi/hr in 4 seconds. The point is that for the same amount of work, power and time are inversely proportional. The power equation suggests that a more powerful engine can do the same amount of work in less time.
A person is also a machine that has a
power rating. Some people are more power-full than others. That is, some people are capable of doing the same amount of work in less time or more work in the same amount of time. A common physics lab involves quickly climbing a flight of stairs and using mass, height and time information to determine a student's personal power. Despite the diagonal motion along the staircase, it is often assumed that the horizontal motion is constant and all the force from the steps is used to elevate the student upward at a constant speed. Thus, the weight of the student is equal to the force that does the work on the student and the height of the staircase is the upward displacement.

Suppose that Ben Pumpiniron elevates his 80-kg body up the 2.0-meter stairwell in 1.8 seconds. If this were the case, then we could calculate Ben's
power rating. It can be assumed that Ben must apply an 800-Newton downward force upon the stairs to elevate his body. By so doing, the stairs would push upward on Ben's body with just enough force to lift his body up the stairs. It can also be assumed that the angle between the force of the stairs on Ben and Ben's displacement is 0 degrees. With these two approximations, Ben's power rating could be determined as shown below.
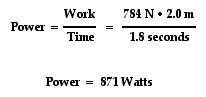
Ben's power rating is 871 Watts. He is quite a
horse.
The expression for power is work/time. And since the expression for work is force*displacement, the expression for power can be rewritten as (force*displacement)/time. Since the expression for velocity is displacement/time, the expression for power can be rewritten once more as force*velocity. This is shown below.


This new equation for power reveals that a powerful machine is both strong (big force) and fast (big velocity). A powerful car engine is strong and fast. A powerful piece of farm equipment is strong and fast. A powerful weightlifter is strong and fast. A powerful lineman on a football team is strong and fast. A
machine that is strong enough to apply a big force to cause a displacement in a s

|
Written on 19.07 by sianturikomkom
In daily life, it is interesting, not only to know the work that can be done, but also the speed or rate the work is done.
The work a person can do is limited not only by the total energy output, but also by the speed that the person is able to transform that energy into an specific work output.
Power can be defined either as the rate at which work is done, or, as the speed of energy transfer per unit time.
Power = W/t = Work/time = transformed energy/time.
In the International System, power is expressed as
Joules per second, unit that receives the name
Watt (W), 1 W = 1J/s.
When we say a small bulb wastes 60 watts, we are saying it transforms 60 Joules of electric energy every second into luminous energy and thermal energy.
For large power measurements we use the Horse Power, abbreviated as Hp, equivalent to 746 Watts.
1 Hp = 746 watts
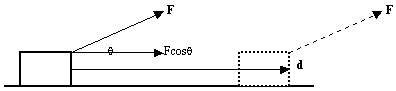
Sometimes it is convenient to express power in terms of the net force F applied to an object and its velocity.
P = W/t, and as W = Fd and v = d/t where d represents displacement, we get,
P = Fv, this is, force times velocity.
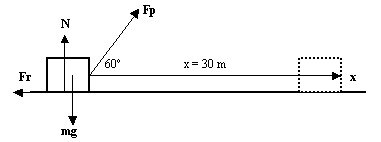
Example 1.
Calculate the power a 1200 kg automobile requires for the following situations:
a) The automobile moves up a long hill inclined 8º with a constant velocity of 12 m/s.
b) The automobile accelerates from 14 m/s to 18 m/s in 10 s to pass another vehicle, on an horizontal road. Suppose a constant friction force for both situations equal to Fr = 500 N.
F denotes the force generated by the engine.
SOLUTION.
a) At constant velocity the acceleration is zero, so we can write:
F = Fr+mgsen
F = 500 N+1200 kg·9,8 m/s2 ·sen8º = 2.137 N
Using P = Fv, results P = 2.137N·12m/s = 25644 Watts, and when expressed in Hp, it is 34,3 Hp.
b) the acceleration is (18m/s-14m/s)/10s = 0,4 m/s2.
By the Second Newton's Law, the sum of all the external forces must be equal to ma, mass times acceleration.
F - Fr = ma
F = 1200kg·0,4m/s2 + 500N = 980 N
The necessary power to reach 18 m/s and pass the other vehicle is
P = Fv = 980N·18m/s = 17.640 Watts or 23,6 Hp.
Example 2.
An elevator whose mass is 1,195 kg can carry passengers with up to 935 kg mass. A 4,255 N constant friction force is opposite to the upward movement, as it is shown in the free body diagram below. a) What is the minimum power required by the engine elevator to make sure to lift the elevator at a constant speed of 4.5 m/s? b) What is the required power when the elevator is designed to develop an upward acceleration of 1.75 m/s2 and the speed is 4.5 m/s?.
Solution:
a) The free body diagram indicates the engine must develop a force T to rise the elevator. f represents the constant friction force and mg, the elevator weight.
Constant speed means zero acceleration, a = 0.
Second Newton' Law states:
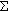 Fy = T - f - mg = ma = 0
Fy = T - f - mg = ma = 0
 T = f + mg
T = f + mg
 T = 4.255x103 N + (2.13x103kg)(9.8m/s2)
T = 4.255x103 N + (2.13x103kg)(9.8m/s2)  T = 2.51x104N
The power P is:
T = 2.51x104N
The power P is:
 P = Tv = (2.51x104 N)(4.5 m/s) = 11.3x104 W
b) Now the engine must do additional work for accelerating the elevator. The only change in the setting of the problem is that a
P = Tv = (2.51x104 N)(4.5 m/s) = 11.3x104 W
b) Now the engine must do additional work for accelerating the elevator. The only change in the setting of the problem is that a  0
0

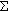 Fy = T - f - mg = ma
Fy = T - f - mg = ma
 T = m(a + g) + f
T = m(a + g) + f
 = (2.13x103kg)(1.75 + 9.8)m/s2 + 4,255 N =
= (2.13x103kg)(1.75 + 9.8)m/s2 + 4,255 N =  = 2.89x104 N
The necessary power P is:
= 2.89x104 N
The necessary power P is:
 P = (2.89x104 N)(4.5 m/s) = 13.0x104 Watts
P = (2.89x104 N)(4.5 m/s) = 13.0x104 Watts

|
![]()

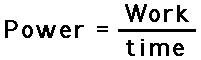

 machine. A car engine is an example of a machine that is given a power rating. The power rating relates to how rapidly the car can accelerate the car. Suppose that a 40-horsepower engine could accelerate the car from 0 mi/hr to 60 mi/hr in 16 seconds. If this were the case, then a car with four times the horsepower could do the same amount of work in one-fourth the time. That is, a 160-horsepower engine could accelerate the same car from 0 mi/hr to 60 mi/hr in 4 seconds. The point is that for the same amount of work, power and time are inversely proportional. The power equation suggests that a more powerful engine can do the same amount of work in less time.
machine. A car engine is an example of a machine that is given a power rating. The power rating relates to how rapidly the car can accelerate the car. Suppose that a 40-horsepower engine could accelerate the car from 0 mi/hr to 60 mi/hr in 16 seconds. If this were the case, then a car with four times the horsepower could do the same amount of work in one-fourth the time. That is, a 160-horsepower engine could accelerate the same car from 0 mi/hr to 60 mi/hr in 4 seconds. The point is that for the same amount of work, power and time are inversely proportional. The power equation suggests that a more powerful engine can do the same amount of work in less time. Suppose that Ben Pumpiniron elevates his 80-kg body up the 2.0-meter stairwell in 1.8 seconds. If this were the case, then we could calculate Ben's power rating. It can be assumed that Ben must apply an 800-Newton downward force upon the stairs to elevate his body. By so doing, the stairs would push upward on Ben's body with just enough force to lift his body up the stairs. It can also be assumed that the angle between the force of the stairs on Ben and Ben's displacement is 0 degrees. With these two approximations, Ben's power rating could be determined as shown below.
Suppose that Ben Pumpiniron elevates his 80-kg body up the 2.0-meter stairwell in 1.8 seconds. If this were the case, then we could calculate Ben's power rating. It can be assumed that Ben must apply an 800-Newton downward force upon the stairs to elevate his body. By so doing, the stairs would push upward on Ben's body with just enough force to lift his body up the stairs. It can also be assumed that the angle between the force of the stairs on Ben and Ben's displacement is 0 degrees. With these two approximations, Ben's power rating could be determined as shown below.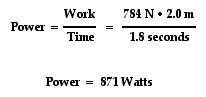




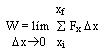
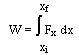
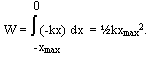
 .
.